Artigo traduzido de Quanta Magazine. Autores: Thomas Lin e Erica Klarreich.
As soluções da Artur Ávila para problemas onipresentes na teoria do caos lhe renderam a primeira medalha Fields do Brasil.

Estava chovendo em um dia frio de primavera e Artur Ávila estava ilhado no campus Jussieu da Universidade de Paris, sem a jaqueta que havia perdido antes de embarcar em Chicago. “Vamos esperar”, disse o matemático brasileiro com voz de sono, vestindo uma camiseta preta confortável revelando o físico aproximado de um robusto meio-campo da Copa do Mundo. “Eu não quero ficar doente”. Em assuntos cotidianos, Ávila fica longe de complicações e riscos. Com medo da ideia de virar sinais de trânsito e tráfego em sentido contrário aos ”mapas unimoidais” e “operadores de Schrödinger quase-periódicos”, ele não dirige nem anda de bicicleta. “Há muitos carros em Paris”, disse ele. “Tenho medo de algum ônibus maluco acabar me matando”.
Logo a conversa se voltou para um tipo diferente de preocupação para Ávila – a lembrança que a aparente falta de realização intelectual pública no Brasil desencoraja os alunos a seguirem carreiras em matemática pura e pesquisa científica. No período que antecedeu a Copa do Mundo esse ano, sites de notícias populares e programas de TV como “Bom Dia Brasil” repetiu a pergunta: Como a sétima economia mundial conseguiu cinco títulos da Copa do Mundo mas zero prêmios Nobel? (O biólogo britânico Peter Medawar tem uma tênue conexão com o Brasil – nasceu no Brasil, mas foi criado pela mãe na Inglaterra). Mesmo a Argentina, rival do Brasil no futebol e com um quinto da população brasileira, possui cinco prêmios Nobel.
Para Ávila, as críticas atrapalham. “Isso não é bom para a auto-imagem do Brasil”, disse ele.
Mesmo assim, em maio, o rapaz natural do Rio de Janeiro tinha uma arma secreta, um argumento convincente de que o Brasil está entre as nações elites na matemática, ao lado da França, Rússia e Estados Unidos. Mas ele não podia contar para ninguém – até ontem. A União Internacional de Matemática fez de Ávila o primeiro brasileiro a receber a Medalha Fields, concedendo ao rapaz o prêmio que muitos consideram ser o equivalente a um prêmio Nobel em matemática, por sua “profunda contribuição para a teoria dos sistemas dinâmicos”, de acordo com o comitê de seleção do prêmio.
“Ele é um dos melhores analistas do mundo”, disse Jean-Christophe Yoccoz, um renomados matemático da Collège de France e medalista Field de 1994. Dos muitos investigadores doutorados talentosos que Yoccoz prestou assessoria, ele disse: “Artur está num nível dele mesmo”. A maioria dos matemáticos foca em um subcampo restrito e acaba tendo pouco sucesso, explicou Yoccoz, mas Ávila “ataca muitos problemas importantes e resolve muitos deles”.
Seu trabalho “não pode ser reduzido a ‘um grande teorema’ pois Artur tem muitos resultados profundos em vários temas diferentes”, disse Marcelo Viana, que trabalhou com Ávila para resolver um problema de longa data sobre o comportamento caótico das bolas de bilhar. Os dois provaram uma fórmula que prevê em qual dos lados da mesa é mais provável que uma bola bata em seguida – e em qual lado ela vai bater depois de milhares ou milhões de tacadas, todas com a mesma margem de erro. Por outro lado, observou Viana, se você tentar prever o tempo “você vai ter boas previsões para amanhã, previsões não muito boas para o dia seguinte e previsões péssimas para daqui 15 dias”.
Messes antes do anúncio de ontem no site da IMU, o dinamicista brasileiro Welington de Melo previu que seu ex-aluno de doutorado ganharia a maior honra da matemática. “Vai ser extremamente importante para o Brasil”, disse ele. “Nunca recebemos um prêmio tão alto. É especialmente importante porque Artur estudou no Brasil o tempo todo”.
Matemática na Praia
Duas coisas que Ávila teme mais do que ônibus irregulares são slides de PowerPoint e formulários de importo de renda. A pressão para aperfeiçoar uma palestra plenária para milhares de presentes no congresso de matemática de 2010 em Hyderabad, Índia, induziu nele uma espécie de paralisia mental, disse ele. Depois de dar uma palestra no Instituto de Tecnologia da Califórnia. Em 2008, ele recusou um honorário de mais de US$2000 só para evitar a papelada.
“Eu seria demitido muito rápido da maioria dos postos de trabalho”, disse ele, acrescentando que ele dorme até bem depois do meio-dia e que ele “não é bom em administrar o tempo”.
Mas em matemática, Ávila tem uma reputação de mergulhar de cabeça em águas desconhecidas e resolver rapidamente uma série de questões ambiciosas em aberto. Seus colegas descrevem seu estilo de trabalho altamente colaborativo e assustadoramente rápido e Ávila se considera como tendo uma intuição e mente clara para simplificar complicações profundas.
“Ele tem uma alta visão geométrica”, disse Raphael Krikorian, um dinamicista armênio-francês da Universidade Pierre e Marie Curie, em Paris. “Ele diz o que você deve olhar, o que você deve fazer. Então, é claro, você tem que trabalhar”.
Agora com a dupla cidadania brasileira e francesa, Ávila passa metade do ano em Paris como diretor de pesquisa do CNRS, a maior organização científica estatal da França, e a outra metade no Rio como bolsista no IMPA, instituto nacional do Brasil para matemática pura e aplicada. (A conexão Brasil-França não é coincidência, em 1970 e 1980, os melhores jovens matemáticos franceses, como Étienne Ghys e Yoccoz, substituíram o serviço militar obrigatório com uma alternativa de serviço público: a realização de pesquisa no IMPA).
Durante os meses de verão e inverno ameno no Rio, Ávila pondera sobre os problemas enquanto está deitado na cama ou perambulando na praia do Leblon a um quarteirão de seu apartamento. Lá, ele tem mais tempo e liberdade para pensar profundamente sobre o seu trabalho e para que as ideias fluam livremente. “Eu não acredito que a solução vai aparecer só se eu bater minha cabeça na parede”, ele gosta de dizer. Às vezes ele convida os colaboradores para o Rio um de cada vez para o que só pode ser descrito como uma experiência de trabalho pouco convencional.
“A última vez que estive no Rio, fiquei em um hotel perto da praia para que eu pudesse trabalhar com ele”, disse Amie Wilkinson, uma matemática da Universidade de Chicago. Depois de procurar Ávila em uma praia que o estava “lotada ombro-a-ombro” de “cariocas sexys demais” e retornar ao seu hotel para tentar chamá-lo, Wilkinson finalmente o encontrou “literalmente, em pé na água”, disse ela. “Nós nos conhecemos e trabalhamos com a água até os joelhos. Foi totalmente louco”.
“Se você trabalha com o Artur”, ela disse, “você tem que colocar uma roupa de banho”.
Ávila é filho de pais que não podiam imaginar seu filho cresceria para se tornar um matemático puro – do qual nunca tinha ouvido falar – e queriam que ele tivesse uma carreira estável como burocrata. A educação formal de seu pai crescido na Amazônia rural só começou na adolescência, mas quando Artur nasceu, seu pai era contador em uma empresa de resseguros do governo, capaz de proporcionar um estilo de vida de classe média no Rio para sua família e comprar livros de matemática para o seu filho quieto, que no início estava mais interessado em ler do que imitar o chute de bicicleta do Pelé. Quando Ávila tinha 6 anos, sua mãe – que ainda arquiva suas declarações de imposto – o matriculou no Colégio de São Bento, uma escola católica conservadora conhecida por seus acadêmicos e pelo Mosteiro de São Bento, do século 16, banhado a ouro. Dois anos depois, seus pais se separaram. Conforme os anos passaram, Ávila focou cada vez mais em matemática, se excluindo de quase tudo – muitas vezes ele foi mal em outras disciplinas e foi expulso depois da oitava série por se recusar a fazer os exames obrigatórios de religião. Ele disse que “deixou a escola completamente despreparado para a interação social normal”.
Ávila teve sua primeira experiência com a comunidade matemática mais ampla pouco antes da expulsão em 1992, quando Luiz Fabiano Pinheiro, um professor mestre em São Bento, carinhosamente conhecido como “Fabiano”, incentivou o prodígio de 13 anos a participar na divisão júnior do prestigiado concurso Olimpíada de Matemática. Ávila estava animado com problemas que nunca tinha encontrado, mas se sentia terrivelmente despreparado. “Pela primeira vez, eu senti que eu não podia fazer nada”, disse ele. No ano seguinte, depois de Fabiano ajuda-lo a se transferir para uma nova escola, Ávila ganhou os prêmios mais importantes em nível estadual. Dois anos mais tarde, ele ficou com o ouro na Olimpíada Internacional de Matemática, em Toronto.
“A primeira vez que encontrei Artur, eu sabia que ele seria proeminente”, disse Fabiano. “Artur foi o melhor de todos os meus alunos”, disse o aposentado de 72 anos de idade, que ensinou durante cinco décadas.
Através das competições de matemática, Ávila descobriu o IMPA, onde o Brasil realizava suas cerimônias de premiação de olimpíada a cada ano. Lá, ele conheceu matemáticos proeminentes como Carlos Gustavo Moreira e Nicolau Corção Saldanha, e ao mesmo tempo tecnicamente na escola, ele começou a estudar matemática em nível de pós-graduação.
Sistemas Dinâmicos
No Brasil, Ávila podia saborear matemática sem as pressões da carreira que ele poderia ter enfrentado nos Estados Unidos. “Foi melhor estudar no IMPA do que se eu estivesse em Princeton ou Harvard”, disse ele. “Crescer e ser educado no Brasil foi muito positivo para mim”.
Um dos principais focos do IMPA está nos sistemas dinâmicos, o ramo da matemática que estuda sistemas que evoluem ao longo do tempo de acordo com um conjunto de regras – uma coleção de planetas que se deslocam em torno de uma estrela, por exemplo, ou uma bola de bilhar que salta ao redor de uma mesa, ou uma população de organismos que cresce ou diminui ao longo do tempo.
Uma das razões porque muitos matemáticos jovens são atraídos para sistemas dinâmicos, diversos pesquisadores dizem, é que um assunto relativamente novo, ao contrário do antigo campo da teoria dos números, e não requer uma grande quantidade de conhecimento teórico prévio para começar a resolver os problemas. E sistemas dinâmicos estão em toda parte na matemática e na natureza. “É como uma cola que une muitos outros assuntos”, disse Krikorian. Nas “duas culturas de matemática” descritas pelo matemático da Universidade de Cambridge e medalhista Fields de 1998 Timothy Gowers, há a teoria de construtores que criam novas matemática e há solucionadores de problemas que analisam questões existentes. A maioria dos dinamicistas, disse Yoccoz, incluindo Ávila e ele próprio, são solucionadores de problemas. “Ambas as formas são necessárias”, disse ele.
Nas décadas anteriores ao trabalho de Ávila, os matemáticos fizeram uma descoberta profunda: para produzir um comportamento complexo, não é necessário começar com regras complexas. Mesmo regras simples quando repetidas uma vez e mais outra, por vezes, produzem o caos: comportamento aparentemente aleatório e imprevisível em que pequenas mudanças nas condições iniciais podem produzir resultados dramaticamente diferentes. Um dos primeiros sistemas simples em que o comportamento caótico foi descoberto é o chamado modelo de “logística” do crescimento da população, o que dá uma formulação precisa de como a população vai mudar de ano para ano. Ávila chegou ao local a tempo de escrever o que poderia ser considerado o capítulo final desta história.
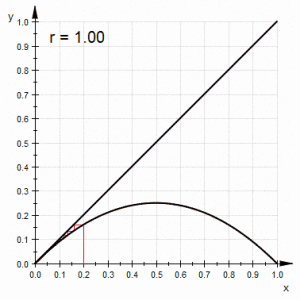
Na natureza, uma pequena população geralmente cresce rapidamente porque há uma abundância de recursos; uma população maior vai crescer mais lentamente, ou mesmo diminuir se os recursos diminuírem. Em 1838, o matemático belga Pierre Verhulst captou esta intuição na equação logística de crescimento populacional. O gráfico da equação logística é simplesmente uma parábola de cabeça para baixo que o aumenta rapidamente se a população é pequena, mas cai precipitadamente se a população é maior do que o meio ambiente pode sustentar. Como uma população muda com o tempo, ela irá se mover na parábola – uma pequena população pode se tornar grande no próximo ano e uma grande pode se tornar pequena.
Nem todas as populações respondem da mesma maneira, é claro. A equação logística codifica essa diversidade com um parâmetro r entre 1 e 4 que controla a inclinação da parábola: maiores valores de R correspondem a populações que reagem mais abruptamente a mudanças extremamente pequenas. As populações com baixos valores de r tenderão a um ponto de equilíbrio ou, talvez, saltitando entre alguns valores de ano para ano. Mas para certos valores de r superiores a cerca de 3,56995 – um valor chamado o “início de caos” – o sistema torna-se completamente imprevisível.
“É apenas uma parábola – algo que as crianças aprendem com a representação gráfica na escola”, observou Wilkinson. “Entretanto, a imagem simples tem essa coisa absurdamente rica acontecendo”.
Os pesquisadores sabiam há décadas que, além do aparecimento do caos, havia “ilhas de estabilidade” – valores de r superiores a 3,56995 para que a população tenderia, por exemplo, a um ciclo de três anos ou um ciclo de sete anos. No final de 1990, Mikhail Lyubich da Stony Brook University, em Long Island, elucidou o que acontece fora destas ilhas: em quase todos os outros parâmetros além do aparecimento do caos, o comportamento da equação é “estocástica”, exibindo o salto imprevisível em torno da marca do caos.
Lyubich tinha terminado recentemente a sua análise da equação logística, quando ele viajou para o IMPA em 1998. Enquanto estava lá, ele conheceu Ávila e imediatamente colocou o tímido rapaz de 19 anos à vontade. “Como estudante, eu estava com medo de errar”, disse Ávila. “Ele foi muito gentil e não assustador”.
Lyubich, de Melo e Ávila decidiram tentar estender a análise do comportamento do Lyubich após o início do caos para uma definição mais geral. Em meados dos anos 1970, os matemáticos descobriram que a mistura particular de ciclos e caos que as exposições equação logística parece ser uma característica universal de todas as famílias de equações com a mesma forma básica como a parábola de cabeça para baixo (chamados mapas unimodais). Os cientistas também descobriram essa mesma combinação de ciclos e do caos em uma ampla variedade de sistemas de dinâmica de fluidos, química e outras áreas da ciência. Os pesquisadores lutaram, porém, para fundamentar as suas observações na matemática formal.
Os três matemáticos investigaram o que acontece a uma família de aplicações unimodais após o início do caos. Eles destilaram o problema a uma questão particular, que Ávila havia então resolvido. Sua construção, Lyubich escreveu em uma pesquisa da obra de Ávila, em 2012, “é delicada e primeiramente parecia bom demais para ser verdade – mas funcionou, e completou o argumento”.
A prova mostrou que uma ampla classe de famílias unimodais se comporta exatamente como a família logística: após o início do caos, há ilhas de estabilidade, rodeadas quase completamente por parâmetros que dão origem a um comportamento estocástico.
Martelo e pregos
Nos meses de outono e primavera, quando ele está baseado no CNRS em Paris, Ávila é um elétron livre da matemática, passando de instituto em instituto em busca de um problema “atrativo”. “Às vezes a beleza se encontra na afirmação matemática e às vezes no uso de ferramentas matemáticas”, disse ele. “Quando elas se misturam de uma forma inesperada, então é nisso que eu quero estar trabalhando.”
Muitos matemáticos são atraídos por Ávila, porque ele “desmistifica” ideias complicadas, fazendo-as parecer triviais, disse Bassam Fayad, um colega do CNRS. “Se você trabalha com ele, essa experiência muda a sua atitude em relação à matemática. Você aprender a fazer contas sem dor”.
Uma vez, enquanto caminhava pelas ruas de Paris com Ávila, Jairo Bochi mencionou que ele estava tentando usar esferas para construir uma prova do que ele estava trabalhando há dois meses. “As pessoas costumam levar muito tempo para entender o seu problema”, disse Bochi, um matemático do sul do Brasil, que dividia um apartamento com Ávila quando estudaram no IMPA. “Ele imediatamente pode ver o que eu estava dizendo e fez uma sugestão: ‘as esferas não vão funcionar; tente um cilindro compacto ‘”. Isso resolveu o problema e, em 2006, publicaram seus resultados.
Ao saltar em um novo campo, Ávila prefere aprender conversando com outras pessoas em vez de ler trabalhos antigos. “Várias vezes eu fui agressivamente para um novo problema sem ter um conhecimento na área”, disse Ávila. “Talvez, não sabendo o que as outras pessoas têm tentado fazer, evito alguns becos sem saída. Assim, quando eu consigo um bom resultado, então estou mais motivado para aprender sobre o campo, para entender o que eu estou provando”.
O centro para a prova nos mapas unimodais era uma técnica poderosa chamada renormalização que às vezes pode converter um sistema dinâmico em um sistema novo, relacionados por zoom em uma pequena parte que se comporta de forma semelhante ao sistema como um todo. Ávila se tornou um mestre da técnica. “Ele contribuiu de forma profunda para a compreensão deste fenômeno”, disse Lyubich.
Renormalização era o martelo de Ávila, e ele começou a perceber que os pregos estavam espalhados em todos os lugares que ele olhava. Ele realizou uma série de novas colaborações em sistemas dinâmicos unimodais, que, Lyubich escreveu na pesquisa, “efetivamente fechou o campo”. Mas isso foi apenas o começo. Ávila começou a mergulhar em outras áreas de sistemas dinâmicos, utilizando renormalização para resolver um problema importante após o outro.
“Parte da força de Ávila é que ele é capaz de trabalhar em todas estas áreas diferentes e, em certo sentido, unificá-los”, disse Lyubich. “Ele seleciona uma área que parece interessante, encontra o problema fundamental para trabalhar, então vai atrás dele e é basicamente imparável”.
Ávila também estudou a evolução de estados quânticos em sistemas físicos regidos por “operadores de Schrödinger quase-periódicos”, que são modelos brutos para quasicristais, estruturas que têm mais ordem do que um líquido, mas menos que um cristal. Para esses operadores de Schrödinger quase-periódicos, Ávila – trabalhando com Svetlana Jitomirskaya da Universidade da Califórnia, Irvine, e David Damanik da Universidade Rice, em Houston – “só veio e limpou”, disse Wilkinson. “Ele respondeu a uma tonelada de perguntas sobre eles”. Uma dessas questões, sobre os estados de energia que os elétrons podem assumir em um modelo específico para um quasicrystal, era conhecido informalmente como o problema “dos dez martinis” porque era tão difícil que o matemático polonês falecido Mark Kac havia prometido 10 martinis para qualquer um que pudesse resolvê-lo. Ávila foi recentemente estendendo esse entendimento para uma família inteira de operadores de Schrödinger quase-periódicos.
Ávila trabalhou com Wilkinson e Sylvain Crovisier da Université Paris-Sud em Orsay, na França, para estudar a famosa hipótese do físico austríaco do século 19, Ludwig Boltzmann. Boltzmann propôs que um gás dentro de uma caixa é “ergódico”, o que significa que os átomos do gás irão rapidamente viajar por todos os arranjos possíveis, em vez de, por exemplo, ficar longos períodos de tempo em determinadas regiões da caixa. Em trabalho recente, Ávila, Crovisier e Wilkinson mostraram que, no caso de modelos matemáticos cujo comportamento é pelo menos moderadamente suave, a hipótese ergódica de Boltzmann é verdadeira, exceto, possivelmente, no caso de alguns sistemas que são altamente previsíveis, semelhantes a uma bola de bilhar saltando ao redor de uma mesa.
Embora a grande maioria de seus trabalhos tenha sido colaborações, passou anos desde que o ex-assessor de doutorado de Ávila trabalhou com ele. “Eu acho que ele é muito rápido para mim”, disse de Melo, “Você tem que trabalhar muito duro para tentar manter-se com ele. Ele ficaria feliz em fazer quase tudo, mas eu quero ter certeza que eu também estou contribuindo”.
Superstar brasileiro
E depois de seu voo transatlântico em maio, barba por fazer, Ávila mais parecia um pós-doc que um dinamicista principal com uma antologia abrangente dos maiores sucessos. Tendo feito contribuições importantes para o seu campo desde que ele tinha 19 anos (e tendo obtido seu doutorado aos 21 anos), ele há muito tempo superou as expectativas. Quando se trata de matemática, se não estiver confuso no trânsito da cidade ou no arquivamento de imposto, as ansiedades tímidas de Ávila são substituídas por uma confiança descontraída e determinação inabalável.
Fayad, que conhece Ávila desde que o prodígio brasileiro chegou pela primeira vez em Paris em 2001, falou da movimentação crescente de seu amigo e seu profissionalismo, se ele está atacando grandes problemas de matemática ou pesquisando técnicas de musculação na Internet. “Ele não é muito amador nas coisas”, disse Fayad. “Suponha que ele quer comer chocolate. Ele vai se tornar um comedor profissional do chocolate”.
Para todas as suas primeiras realizações, Ávila insiste que ele não estabelece metas para si mesmo, preferindo deixar que o seu trabalho se desenrolasse naturalmente. “Na maioria das vezes, quando eu realizo alguma coisa, não é porque eu tinha um objetivo, mas porque eu estava fazendo algo que eu queria fazer”, disse ele. “Eu só quero continuar curtindo fazer matemática”.
E ele espera que seu país compartilhe seu entusiasmo. Além da Medalha Fields que Ávila ganhou este ano, o Brasil será a sede da Olimpíada Internacional de Matemática em 2017 e do Congresso Internacional de Matemáticos em 2018, onde as próximos medalhas Fields serão anunciado. “Estes quatro anos, naturalmente, serão um bom período para desenvolver a matemática no Brasil”, disse Ávila.
Ele espera que seja apenas o início de um movimento de transformação que vai elevar a promessa intelectual de seu país.
No ano passado, em um pequeno bar em Paris, onde começou a tocar uma música brasileira, Ávila vê um matemático francês dizer a seus amigos que o Brasil “não tem realmente uma escola de matemática.” Quando Ávila se opôs, outro matemático deixou claro que ele estava ciente do IMPA.
“Eu estava um pouco irritado e insisti que uma matemática de alto nível que vinha de lá”, disse Ávila, para o qual o matemático francês respondeu: sim, aí está o astro brasileiro – Ávila ou algo assim. “Ele estava esperando alguém mais velho”.

